20. Matrices in Python
Vector versus Matrix
Vectors are one part of the Kalman filter equations. But you also need to be able to use matrices.
You've seen how Python can represent a vector in a list. A vector can be thought of like a simple grid with one row and a column for each element. If you thought of a vector like a grid, the vector \begin{bmatrix}17, 25, 6, 2\end{bmatrix} would be represented like this:
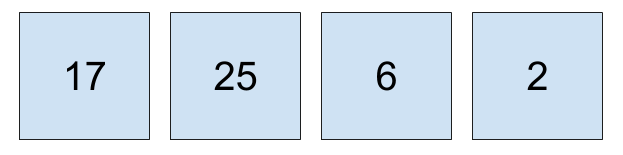
But you could also call this vector a matrix. This four element vector is a one by four matrix or 1x4. The one represents the number of rows and the four represents the number of columns.
What if you rotated the boxes around so that they looked like this?
\begin{bmatrix}17 \\ 25 \\ 6 \\ 2 \end{bmatrix}
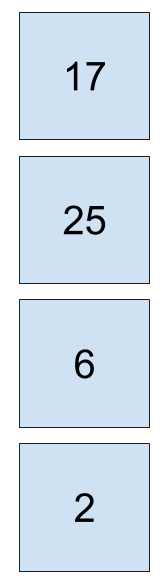
Rotated Vector
SOLUTION:
YesVector as a Matrix
SOLUTION:
4 rows, 1 columnTwo Vectors
What happens if you take a vector and duplicate the vector like this?
\begin{bmatrix}17 &17 \\ 25 & 25 \\ 6 & 6 \\ 2 & 2\end{bmatrix}
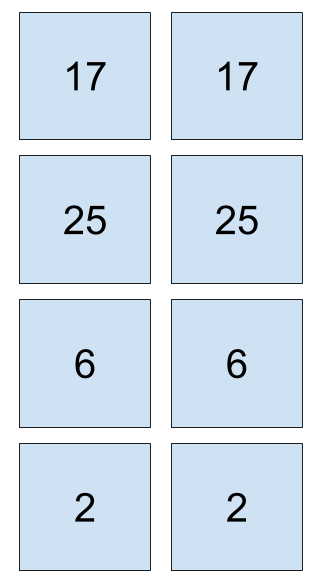
Now, you have 4 rows and 2 columns for a 4x2 matrix. What about duplicating the horizontal vector?
\begin{bmatrix}17 & 25 & 6 & 2 \\ 17 & 25 & 6 & 2\end{bmatrix}
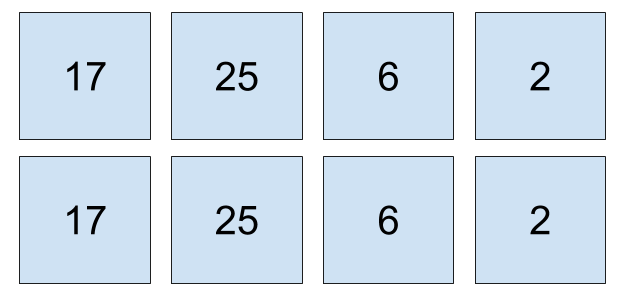
Matrix Size
SOLUTION:
2x4Representing a Matrix in Python
A matrix is thus a two-dimensional grid with m rows and n columns. Take a look at this matrix, which is a little larger than the examples so far.
\begin{bmatrix}17 & 25 & 6 & 2 & 16 \\ 6 & 1 & 8 & 4 & 22 \\17 & 8 & 54 & 15 & 65 \\11 & 25 & 68 & 9 & 2\end{bmatrix}
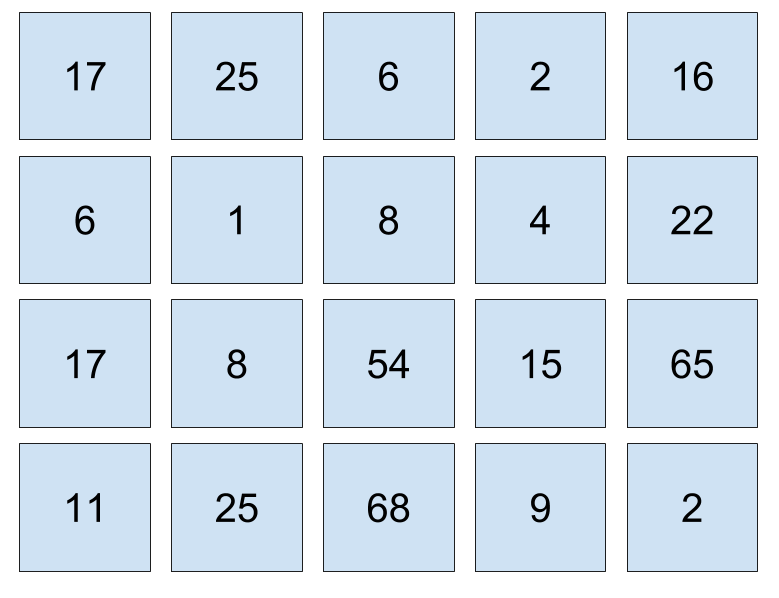
This matrix is 4x5; the matrix has 4 rows and 5 columns.
How would you represent a matrix like this in Python? Start with the top row \begin{bmatrix}17, 25, 6, 2, 16\end{bmatrix}. When looking at the top row alone, it looks like a vector. And in Python, you were using lists to represent vectors.
When representing matrices in Python, you can think of each row as a vector:
first_row = [17, 25, 6, 2, 16]What about the second row?
second_row = [6, 1, 8, 4, 22]And so on:
third_row = [17, 8, 54, 15, 65]
fourth_row = [11, 25, 68, 9, 2]Representing All Rows with One Variable
You are representing each row with its own variable. The next step is to represent the entire matrix with only one variable.
If you list all of the rows one after another, you get a list of lists:
matrix = [first_row, second_row, third_row, fourth_row]The "matrix-ness" is more explicit if you write it like this:
matrix = [
first_row,
second_row,
third_row,
fourth_row
]Replacing the variables with the vectors gives you a big list of lists:
matrix = [[17, 25, 6, 2, 16],
[6, 1, 8, 4, 22],
[17, 8, 54, 15, 65],
[11, 25, 68, 9, 2]]or, slightly cleaner:
matrix = [
[17, 25, 6, 2, 16],
[6, 1, 8, 4, 22],
[17, 8, 54, 15, 65],
[11, 25, 68, 9, 2]
]Matrix Access
SOLUTION:
68Coding Vectors as Matrices
SOLUTION:
x = [[1, 5, 9, 3, 1]]Practice with Coding Matrices
In the next part of the lesson, you will practice coding matrices in Python.